Kita akan memulai pembahasan ini dengan menurunkan rumus-rumus untuk sin 2A dan cos 2A dengan menggunakan rumus-rumus sin (A + B) dan cos (A + B). Rumus-rumus untuk sin 2A dan cos 2A disebut sebagai rumus-rumus sudut rangkap. Berikut ini dijabarkan bagaimana kita menurunkan rumus sin 2A.

Baris terakhir tersebut memberikan kita rumus sudut rangkap yang pertama.

Hal pertama yang harus dicatat pada rumus di atas adalah bahwa 2 pada sin 2A tidak dapat difaktorkan keluar dan ditulis sebagai koefisien. Apabila dituliskan,

Sebagai contoh, jika A = 30°, sin 2 ∙ 30° = sin 60° = √3/2, yang tidak sama dengan 2 sin 30° = 2 ∙ ½ = 1.
Contoh 1: Menentukan Nilai Sinus Sudut Rangkap
Jika sin A = 4/5 dengan A berada pada kuadran II, tentukan sin 2A.
Pembahasan Untuk menerapkan rumus sin 2A, pertama kita harus tentukan nilai cos Aterlebih dahulu. Karena A terletak pada kuadran II, maka nilai cos A negatif.

Sekarang kita dapat menerapkan rumus sin 2A.

Kita juga dapat menggunakan rumus sudut rangkap untuk membuktikan suatu identitas trigonometri.
Contoh 2: Membuktikan Identitas Trigonometri
Buktikan (sin θ + cos θ)² = 1 + sin 2θ.
Pembahasan Untuk membuktikan identitas ini, pertama kita ekspansi bentuk yang ada pada ruas kiri.

Contoh 3: Membuktikan Identitas Trigonometri
Buktikan bahwa,

Pembahasan Karena bentuk yang ada pada ruas kanan lebih rumit daripada yang sebelah kiri, maka kita membuktikan identitas ini dari ruas kanan.
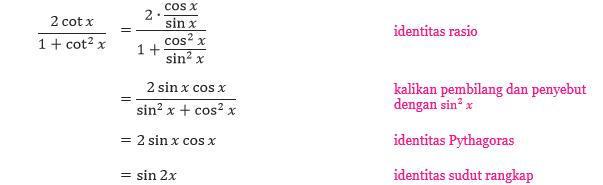

Baris terakhir tersebut memberikan kita rumus sudut rangkap yang pertama.

Hal pertama yang harus dicatat pada rumus di atas adalah bahwa 2 pada sin 2A tidak dapat difaktorkan keluar dan ditulis sebagai koefisien. Apabila dituliskan,

Sebagai contoh, jika A = 30°, sin 2 ∙ 30° = sin 60° = √3/2, yang tidak sama dengan 2 sin 30° = 2 ∙ ½ = 1.
Contoh 1: Menentukan Nilai Sinus Sudut Rangkap
Jika sin A = 4/5 dengan A berada pada kuadran II, tentukan sin 2A.
Pembahasan Untuk menerapkan rumus sin 2A, pertama kita harus tentukan nilai cos Aterlebih dahulu. Karena A terletak pada kuadran II, maka nilai cos A negatif.

Sekarang kita dapat menerapkan rumus sin 2A.

Kita juga dapat menggunakan rumus sudut rangkap untuk membuktikan suatu identitas trigonometri.
Contoh 2: Membuktikan Identitas Trigonometri
Buktikan (sin θ + cos θ)² = 1 + sin 2θ.
Pembahasan Untuk membuktikan identitas ini, pertama kita ekspansi bentuk yang ada pada ruas kiri.

Contoh 3: Membuktikan Identitas Trigonometri
Buktikan bahwa,

Pembahasan Karena bentuk yang ada pada ruas kanan lebih rumit daripada yang sebelah kiri, maka kita membuktikan identitas ini dari ruas kanan.
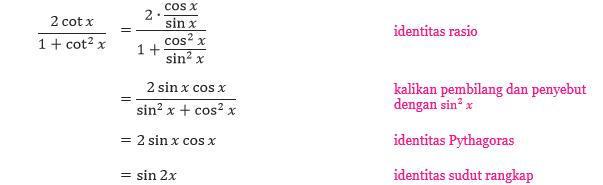
Sumber:
yos3prens.wordpress.com