Pengertian dan Nilai Suku Banyak
Pengertian Suku Banyak
Suku banyak adalah suatu bentuk yang memuat variabel berpangkat. Suku banyak dalam x berderajat n dinyatakan dengan:
Dengan syarat: n bagian dari bilangan cacah dan an, an – 1, … , a0 disebut koefisien-koefisien suku banyak, a0 disebut suku tetap dan an ≠ 0
Contoh
1) 6×3 – 3×2 + 4x – 8 adalah suku banyak berderajat 3, dengan koefisien x3 adalah 6,koefisien x2 adalah –3, koefisien x adalah 4, dan suku tetapnya –8.
2) 2×2 – 5x + 4 – 7/x adalah bukan suku banyak karena memuat pangkat negatif yaitu 7/x atau
7x–1 dengan pangkat –1 bukan anggota bilangan cacah.
f(x) = anxn + an – 1xn – 1 + an – 2xn – 2 + … + a1x + a0, di mana n bagian dari bilangan cacah dan an ≠ 0. Nilai f(x) tersebut merupakan nilai suku banyak. Untuk menentukan nilai suku banyak dapat dilakukan dengan dua cara berikut :
1) Cara substitusi
Misalkan suku banyak f(x) = ax3 + bx2 + cx + d. Jika nilai x diganti k, maka nilai suku banyak f(x) untuk x = k adalah f(k) = ak3 + bk2 + ck + d. Agar lebih memahami tentang cara substitusi, pelajarilah contoh soal berikut ini.
1) 6×3 – 3×2 + 4x – 8 adalah suku banyak berderajat 3, dengan koefisien x3 adalah 6,koefisien x2 adalah –3, koefisien x adalah 4, dan suku tetapnya –8.
2) 2×2 – 5x + 4 – 7/x adalah bukan suku banyak karena memuat pangkat negatif yaitu 7/x atau
7x–1 dengan pangkat –1 bukan anggota bilangan cacah.
b. Nilai Suku Banyak
Suku banyak dengan derajat n dapat dinyatakan sebagai suatu fungsi f(x) berikut ini.f(x) = anxn + an – 1xn – 1 + an – 2xn – 2 + … + a1x + a0, di mana n bagian dari bilangan cacah dan an ≠ 0. Nilai f(x) tersebut merupakan nilai suku banyak. Untuk menentukan nilai suku banyak dapat dilakukan dengan dua cara berikut :
1) Cara substitusi
Misalkan suku banyak f(x) = ax3 + bx2 + cx + d. Jika nilai x diganti k, maka nilai suku banyak f(x) untuk x = k adalah f(k) = ak3 + bk2 + ck + d. Agar lebih memahami tentang cara substitusi, pelajarilah contoh soal berikut ini.
Contoh soal
Hitunglah nilai suku banyak berikut ini untuk nilai x yang diberikan.
1. f(x) = 2×3 + 4×2 – 18 untuk x = 3
2. f(x) = x4 + 3×3 – x2 + 7x + 25 untuk x = –4
Penyelesaian :
1. f(x) = 2×3 + 4×2 – 18
f(3) = 2 . 33 + 4 . 32 – 18
= 2 . 27 + 4 . 9 – 18
= 54 + 36 – 18
f(3) = 72
Jadi, nilai suku banyak f(x) untuk x = 3 adalah 72.
Hitunglah nilai suku banyak berikut ini untuk nilai x yang diberikan.
1. f(x) = 2×3 + 4×2 – 18 untuk x = 3
2. f(x) = x4 + 3×3 – x2 + 7x + 25 untuk x = –4
Penyelesaian :
1. f(x) = 2×3 + 4×2 – 18
f(3) = 2 . 33 + 4 . 32 – 18
= 2 . 27 + 4 . 9 – 18
= 54 + 36 – 18
f(3) = 72
Jadi, nilai suku banyak f(x) untuk x = 3 adalah 72.
2. f(x) = x4 + 3×3 – x2 + 7x + 25
f(–4) = (–4)4 + 3⋅ (–4)3 – (–4)2 + 7 ⋅ (–4) + 25
= 256 – 192 – 16 – 28 + 25
f(–4) = 45
f(–4) = (–4)4 + 3⋅ (–4)3 – (–4)2 + 7 ⋅ (–4) + 25
= 256 – 192 – 16 – 28 + 25
f(–4) = 45
Jadi, nilai suku banyak f(x) untuk x = –4 adalah 45.Pembagian suku banyak hampir sama dengan pembagian bilangan. Ketika kita membagi 46 dengan 5, hasil baginya adalah 9 dan sisanya adalah 1.

atau,
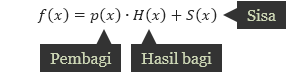
Suku banyak p(x) disebut sebagai pembagi, H(x) merupakan hasil bagi, dan S(x) merupakan sisa.
Contoh 1: Pembagian Bersusun Suku Banyak
Bagilah 4x² – 14x + 15 dengan x – 4. Nyatakan hasilnya ke dalam masing-masing bentuk yang ditunjukkan pada Algoritma Pembagian.
Pembahasan Suku banyak yang akan dibagi adalah 4x² – 14x + 15, dan pembaginya x – 4. Pertama kita susun kedua suku banyak tersebut sebagai berikut.

Selanjutnya kita bagi suku pertama terbagi dengan suku pertama pembagi untuk mendapatkan suku pertama hasil bagi: 4x²/x = 4x. Kemudian kita kalikan pembagi dengan 4x dan kita kurangkan terbagi dengan hasil yang diperoleh.

Kita ulang proses ini dengan menggunakan baris terakhir 2x + 15 sebagai yang terbagi.

Proses pembagian berakhir ketika baris terakhir memiliki derajat yang kurang dari derajat pembagi. Baris terakhir merupakan sisa, sedangkan baris yang paling atas merupakanhasil bagi. Pembagian di atas dapat dinyatakan dalam dua bentuk berikut.

Algoritma Pembagian
Jika f(x) dan p(x) adalah suku banyak, dengan p(x) ≠ 0, maka ada suku banyak tunggalH(x) dan S(x), di mana S(x) adalah 0 atau suku banyak yang memiliki derajat kurang dari derajat p(x), sedemikian sehingga
atau,
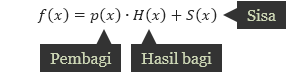
Suku banyak p(x) disebut sebagai pembagi, H(x) merupakan hasil bagi, dan S(x) merupakan sisa.
Contoh 1: Pembagian Bersusun Suku Banyak
Bagilah 4x² – 14x + 15 dengan x – 4. Nyatakan hasilnya ke dalam masing-masing bentuk yang ditunjukkan pada Algoritma Pembagian.
Pembahasan Suku banyak yang akan dibagi adalah 4x² – 14x + 15, dan pembaginya x – 4. Pertama kita susun kedua suku banyak tersebut sebagai berikut.

Selanjutnya kita bagi suku pertama terbagi dengan suku pertama pembagi untuk mendapatkan suku pertama hasil bagi: 4x²/x = 4x. Kemudian kita kalikan pembagi dengan 4x dan kita kurangkan terbagi dengan hasil yang diperoleh.

Kita ulang proses ini dengan menggunakan baris terakhir 2x + 15 sebagai yang terbagi.

Proses pembagian berakhir ketika baris terakhir memiliki derajat yang kurang dari derajat pembagi. Baris terakhir merupakan sisa, sedangkan baris yang paling atas merupakanhasil bagi. Pembagian di atas dapat dinyatakan dalam dua bentuk berikut.

Sumber:
yos3prens.wordpress.com